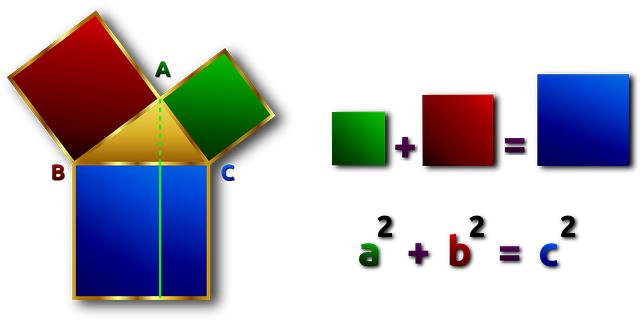Pythagorova a Euklidovy Věty: Matematika, Která Vás Dostane na Vysokou

Víte, co mají společného legendární Pythagoras a Euklides s matematikou, kterou byste měli znát? Pokud si myslíte, že se jedná jen o dávné teorie, tak se mýlíte! Jejich věty mají význam i dnes a mohou vás dostat až na vysokou úroveň matematického myšlení. Podívejme se společně na to, jak tyto matematické génie ovlivnili naše chápání světa kolem nás.

Pythagorova věta: Základ k pochopení geometrie

Pythagorova věta je jedním z nejdůležitějších matematických principů, který nám pomáhá porozumět vztahům mezi délkami stran pravoúhlých trojúhelníků. Tato věta říká, že druhá mocnina délky přepony je rovna součtu druhých mocnin délek obou odvěsen trojúhelníka. Díky této větě můžeme řešit mnoho geometrických úloh a aplikací ve fyzice, inženýrství a dalších oborech.

Euklidova věta, která je založena na Pythagorově větě, nám poskytuje komplexnější pohled na vztahy v pravoúhlých trojúhelnících. Tato věta nás učí, jakým způsobem lze sestrojit pravidelný šestúhelník pomocí pravoúhlého trojúhelníka. Díky těmto matematickým principům můžeme lehce porozumět geometrii a aplikovat ji v různých situacích.

V kombinaci s dalšími matematickými znalostmi a dovednostmi, jako je trigonometrie a algebra, můžeme díky Pythagorově a Euklidově větě skvěle porozumět geometrii a matematice jako celku. Tyto věty nám pomáhají vytvářet nové poznatky a objevovat nové principy, které obohacují naše chápnutí světa kolem nás.

Euklidovy věty: Proč jsou stále relevantní

Euklidovy věty jsou jedny z nejznámějších matematických teorií a jejich relevanci nelze přecenit. Tyto věty, společně s Pythagorovou větou, jsou základními kameny geometrie a matematiky jako takové. Zajímavé je, že i po tisíciletích od jejich vzniku jsou stále důležité a používané ve mnoha oblastech.

Pythagorova věta, která říká, že ve čtverci nad přeponou pravoúhlého trojúhelníka je suma ploch čtverců nad odvěsnami, je jedním z nejznámějších matematických tvrzení. Euklidovy věty, které se zabývají geometrií a základy matematiky, dodnes slouží jako základní pilíře výuky matematiky a budování složitějších geometrických struktur.

Je fascinující sledovat, jak tyto věty stále ovlivňují naše myšlení a pozitivně přispívají k rozvoji matematického myšlení. Proto je důležité nezapomínat na jejich relevanci a význam, ať už se zabýváte matematikou profesionálně, nebo se jí jen vášnivě zajímáte.

Matematické zkoumání: Jak se dostat na vysokou úroveň

Pythagorova a Euklidovy věty patří mezi základní principy geometrie a matematiky, které nás mohou přivést na vysokou úroveň porozumění této vědecké disciplíny. Známé jako zákony pythagorovské trojice a základy planimetrie, tyto věty jsou klíčové pro pochopení vztahů mezi stranami a úhly ve tvaru, a tím i pro řešení složitějších matematických problémů.

Pokud chcete dosáhnout hlubšího chápání matematiky a zvyšovat svou vlastní úroveň znalostí, je nezbytné porozumět těmto základním matematickým principům. Studium Pythagorovy a Euklidovy věty není jen nutností pro studenty matematiky, ale může také sloužit jako inspirace pro každého, kdo se zajímá o logické myšlení, důkazování a abstraktní myšlení.

Prozkoumejte tabulku níže, která přehledně ukazuje klíčové prvky Pythagorovy a Euklidovy věty a pomůže vám lépe porozumět jejich významu a použití ve světě matematiky:

Princip	Popis
Pythagorova věta	Stanovuje vztah mezi délkami stran pravoúhlého trojúhelníka: a2 + b2 = c2
Euklidovy věty	Obsahují postupy a důkazy týkající se geometrických útvarů a vztahů mezi nimi

Nejoblíbenější matematické teorie: Čím vás uchvátí Pythagoras a Euklid

Pythagorova věta je jednou z nejoblíbenějších teorií v matematice, která nás fascinuje svou jednoduchostí a zároveň širokým využitím v různých oblastech. Tato věta se zabývá vztahem mezi délkami stran pravoúhlého trojúhelníka a je stále důležitou součástí výuky matematiky po celém světě. Pythagoras dokázal, že čtverec nad přeponou pravoúhlého trojúhelníka je roven součtu čtverců nad oběma odvěsnami.

Euklidovy věty jsou dalšími matematickými teoriemi, které nás zaujmou svou precizností a logickým postupem. Euklidovy teorie se zaměřují na geometrické konstrukce a důkazy, které jsou pevně zakořeněny v axiomech a postulátech. Jeho práce zahrnují mnoho základních pravidel pro práci s přímky, úhly a kružnicemi, což je klíčové pro porozumění geometrii a matematice jako celku.

Obě tyto matematické teorie – Pythagorova věta i Euklidovy věty – nám ukazují, jak matematika dokáže vysvětlit a popsat různé jevy a situace ve světě kolem nás. Jejich síla spočívá v precizním myšlení a logickém uvažování, což dělá z matematiky fascinující a univerzální disciplínu.

Nepostradatelné znalosti pro každého milovníka matematiky

Pythagorova věta je jednou z nejznámějších vět v matematice a klade důraz na vztah mezi délkami stran pravoúhlého trojúhelníka. Tato věta je základním kamenem pro pochopení geometrie a mnoha dalších matematických konceptů. Bez znalosti této věty by nebylo možné porozumět mnoha matematickým principům a aplikacím.

Euklidovy věty jsou další důležitou součástí matematické teorie a zabývají se například vztahem mezi stranami a úhly ve trojúhelníku či geometrickými konstrukcemi. Tyto věty poskytují základní návody pro řešení problémů a analýzu geometrických útvarů. Bez znalostí Euklidových vět by bylo obtížné porozumět složitějším matematickým úlohám a teoriím.

Právě proto jsou tyto znalosti nepostradatelné pro každého milovníka matematiky, neboť poskytují pevný základ pro pochopení a aplikaci matematických principů a konceptů. Bez znalosti těchto vět by matematické studium ztratilo svou hloubku a krásu, a tak je důležité se s nimi blíže seznámit a pochopit jejich důležitost.

Významné využití Pythagorovy a Euklidovy matematiky v praxi

Pythagorova a Euklidovy věty jsou základními principy matematiky, které mají široké využití v praxi. Známé Pythagorovy věty se může zdát jako pouhá abstraktní koncepce, ale ve skutečnosti jsou klíčové pro mnohé oblasti lidské činnosti. Zde je pár významných aplikací těchto matematických principů:

• Stavebnictví: Pythagorova věta je základním nástrojem pro výpočet délek stran pravoúhlých trojúhelníků, což je důležité pro navrhování a konstrukci budov a infrastruktury.
• Technologie: Euklidovy věty jsou klíčové při navrhování algoritmů a programování softwaru, zejména v oblasti počítačové grafiky a kryptografie.
• Fyzika: Matematické principy Pythagorovy a Euklidovy geometrie jsou nezbytné pro formulaci fyzikálních zákonů a rovnice, které popisují přírodní jevy a procesy.

Využití Pythagorovy a Euklidovy matematiky v praxi je tak skutečně důležité a rozmanité, což jen dokazuje, jak hluboký a univerzální je vliv těchto starověkých matematických konceptů na každodenní život a technologický pokrok.

Inspirace matematických génioů: Proč byste neměli podceňovat Pythagorův a Euklidův dědictví

Pythagorova a Euklidovy Věty: Matematika, Která Vás Dostane na Vysokou

Pythagorova věta a Euklidovy postuláty mohou na první pohled působit jako zbytečné informace z minulosti, ale ve skutečnosti jsou základními pilíři moderní matematiky. Tyto starověké myšlenky nejenže posunuly svět dopředu, ale stále mají obrovský vliv na současnou vědu a technologii. Zde je pár důvodů, proč byste neměli podceňovat dědictví Pythagora a Euklida:

• Geometrie ve vašem každodenním životě: Pythagorova věta není jen nudný koncept z matematiky, ale skutečně se uplatňuje v mnoha situacích okolo nás. Od navrhování domů po výpočet vzdálenosti mezi dvěma body – Pythagorova věta je všudypřítomná.
• Základy moderní algebry: Euklidovy postuláty mohou být považovány za pravidla hry, která jsou nezbytná k vytvoření složitějších matematických konceptů. Bez nich by nebylo možné chápat algebraické rovnice a operace.
• Vliv na technologii: Máte rádi počítače nebo moderní mobilní telefony? Tyto technologie jsou postaveny na základech matematiky, kterou formulovali Pythagoras a Euklides. Jejich dědictví je stále silně přítomné v našem každodenním životě.

Klíčové Poznatky

Doufáme, že vás náš článek o Pythagorových a Euklidových větách zaujal a inspiroval k prozkoumání fascinujícího světa matematiky. Jak vidíte, matematika je všude kolem nás a může nás opravdu dostat na vysokou úroveň. Pokud máte jakékoliv dotazy nebo zájem o další matematická témata, neváhejte nás kontaktovat. Děkujeme za váš zájem a přejeme vám mnoho úspěchů ve vašich matematických dobrodružstvích!